leetcode4_寻找两个有序数组的中位数

1.题目描述

给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。

请你找出这两个有序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。

你可以假设 nums1 和 nums2 不会同时为空。

示例1:

nums1 = [1, 3]
nums2 = [2]

则中位数是 2.0

示例2:

nums1 = [1, 2]
nums2 = [3, 4]

则中位数是 (2 + 3)/2 = 2.5

2.解题分析

先从题干进行分析 , 本题若没有时间复杂度要求,将是一道极简单的题.

我们可以先将两个数组合并,再排序 ,以此完成解题.

本题给出的时间复杂度为 O(log(m + n)) , 由此我们想到二分查找,事实也确乎如此.

下面开始分析问题,先从中位数的作用入手

中位数 : 将一个集合划分为两个长度相等的子集，其中一个子集中的元素总是大于另一个子集中的元素。

对本题而言,我们要做的就是把有序数组A,B进行分割,共分为四个子数组,分别记作left_A,left_B,left_A,right_A.

将left_A和left_B合并记作left_part,

同理,得到right_part.

如果我们可以确认:

1. len(left_part) = len(right_part)
2. max(left_part) ≤ min(right_part)

那么,我们就得到了两个长度相同的部分,且其中一部分的元素总是大于或等于另一部分的元素.

到这里,我们就已经很接近答案了.

要满足上面的两个条件,我们只需要保证：

注意: 其中1中的 m - i + n - j + 1的 "+1"的原因是存由于在奇偶的差别.

从1中我们可以看出,j 可以被 i 表示,所以,接下来的问题变为:

找到满足2的 i

对此,我们可以使用二分查找(具体查找的过程,以及临界分析写在下面注释中)

当找到目标对象 i 后 , 中位数为 :

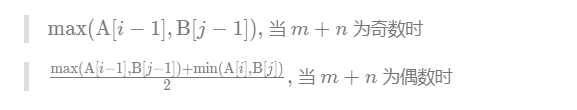
3.代码实现

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int m = nums1.length;
        int n = nums2.length;
        // 保证num1的长度总是小于或等于nums2
        if(m>n){
            int[] temp = nums1;nums1 = nums2; nums2 = temp;
            int lengthTemp = m; m = n; n = lengthTemp;
        }
        int imax = m,imin = 0,half = (m+n+1)/2 ;
        //开始查找
        while(imax >= imin){
            int i = (imax+imin)/2;
            int j = half - i;
            // i 过小且i可以再增大
            if(i<imax && nums2[j-1]>nums1[i]){
                imin = i +1;
            }
            // i 过大且i可以再减小
            else if(i>imin && nums1[i-1]>nums2[j]){
                imax = i -1;
            }
            else{
                int leftmax = 0;
                // left_num1为空时
                if(i == 0) {leftmax = nums2[j-1];}
                // left_num2为空时
                else if(j == 0){ leftmax = nums1[i-1];}
                else {leftmax = Math.max(nums1[i-1],nums2[j-1]);}
                // 当m+n 为奇数时,返回奇数解
                if((m+n)%2 == 1)  return leftmax;
                
                int rightmin = 0;
                // right_num1为空时
                if(i == m){ rightmin = nums2[j];}
                // right_num2为空时
                else if(j == n) {rightmin = nums1[i];}
                else{ rightmin = Math.min(nums1[i],nums2[j]);}
                // 当m+n 为偶数时,返回偶数解
                return (leftmax+rightmin)/2.0;
            }
        }        
        return 0.0;
    }
}