二叉排序树及二叉树常见算法

发表于 | 阅读数
字数统计: 1.3k | 阅读时长 ≈ 7

二叉排序树及二叉树常见算法

一、定义

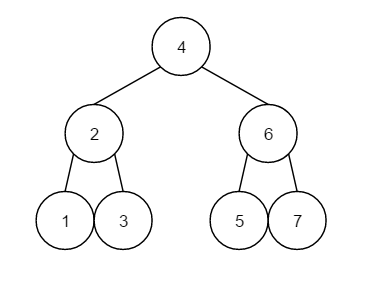
二叉排序树，又叫二叉查找树，它或者是一棵空树；或者是具有以下性质的二叉树：

  1. 若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值；

  2. 若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值；

  3. 它的左右子树也分别为二叉排序树。

    如下图：

image-20191222152211471

二、基本方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
//定义
class BSNode{
	public int data;
	public BSNode left;
	public BSNode right;
	public BSNode(int data){
		this.data=data;
		this.left=null;
		this.right=null;
	}
	
}
//二叉排序树
public class BinarySortTree {
	private BSNode root;
	public BSNode getRoot() {
		return root;
	}
	public BinarySortTree(){
		root=null;
	}
	//插入数据到二叉树中
	public void insert (int data){
		BSNode newNode=new BSNode(data);
		if(root==null){
			root=newNode;
		}
		else{
			BSNode cNode=root;
			BSNode parent;
			while(true){
				parent=cNode;
				if(data<cNode.data){
					cNode=cNode.left;
					if(cNode==null){
						parent.left=newNode;
						return;
					}
				}else{
					cNode=cNode.right;
					if(cNode==null){
						parent.right=newNode;
						return;
					}
					
				}
				
			}
			
		}
	}
	//以数组形式构建二叉树
	public void buildTree(int []data){
		for(int i=0;i<data.length;i++){
			insert(data[i]);
		}
	}
	//中序遍历
	//实现前序和后续只需要更改顺序即可
	public void inOrder(BSNode localRoot){
		if(localRoot!=null){
			inOrder(localRoot.left);
			System.out.print(localRoot.data+" ");
			inOrder(localRoot.right);
		}
	}
	public void preOrder(BSNode localRoot){
		if(localRoot!=null){
			System.out.print(localRoot.data+" ");
			preOrder(localRoot.left);
			preOrder(localRoot.right);
		}
	}
	public void AfterOrder(BSNode localRoot){
		if(localRoot!=null){
			AfterOrder(localRoot.left);
			AfterOrder(localRoot.right);
			System.out.print(localRoot.data+" ");
		}
	}
	public static void main(String[] args) {
		BinarySortTree bs=new BinarySortTree();
		int data[]=new int[]{2,8,7,4,9,3,1,6,7,5};
		bs.buildTree(data);
		System.out.println("中序遍历");
		bs.inOrder(bs.getRoot());
		System.out.println("\n前序遍历");
		bs.preOrder(bs.getRoot());
		System.out.println("\n后序遍历");
		bs.AfterOrder(bs.getRoot());
	}

}

输出结果：

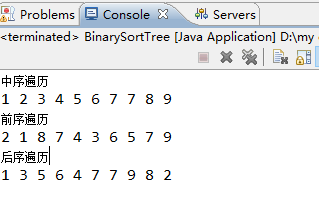
image-20191222162250213

三、如何层序遍历二叉树

可以使用队列来实现二叉树的层序遍历。其主要思想如下：现将根结点放在队列中，然后每次都从队列中取出一个结点打印打印该结点的值，若这个结点有子结点，则将他的子结点放在队列尾，直到队列为空。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//层序遍历
	public void layerTranverse(){
		if(this.root==null){
			return;
		}
		Queue <BSNode> q=new LinkedList<BSNode>();
		q.add(this.root);
		while(!q.isEmpty()){
			BSNode n=q.poll();
			System.out.print(n.data+" ");
			if(n.left!=null)
				q.add(n.left);
			if(n.right!=null)
				q.add(n.right);
		}
		
	}

四、 二叉树的最大深度

1
2
3
4
5
6
7
8
public int maxDepth(TreeNode root) {
        if(root==null){
            return 0;
        }
        int left = maxDepth(root.left);
        int right = maxDepth(root.right);
        return Math.max(left,right)+1;
    }

五、二叉树的镜像

1
2
3
4
5
6
7
8
9
10
11
12
public void Mirror(TreeNode root) {
        if(root!=null){
            if(root.left!=null || root.right!= null){
                TreeNode temp =root.left;
                root.left=root.right;
                root.right=temp;
            }
            Mirror(root.left);
            Mirror(root.right);
        }
       
}

六、 对称二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
boolean isSymmetrical(TreeNode pRoot){
        if(pRoot == null)
            return true;
        return real(pRoot.left,pRoot.right);
    }
    public boolean real(TreeNode root1,TreeNode root2){
        if(root1 == null && root2 == null){
            return true;
        }
        if(root1 ==null || root2 == null){
            return false;
        }
        if(root1.val != root2.val){
            return false;
        }
        return real(root1.left,root2.right)&&real(root1.right,root2.left);

七、路径总和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public class Solution {
    private ArrayList<Integer> list = new ArrayList<Integer>();
    private ArrayList<ArrayList<Integer>> listAll = new ArrayList<ArrayList<Integer>>();
    public ArrayList<ArrayList<Integer>> FindPath(TreeNode root,int target) {
        if(root == null)
            return listAll;
        list.add(root.val);
        target -= root.val;
        if(target == 0 && root.left==null && root.right == null){
            listAll.add(new ArrayList<Integer>(list));
        }
        FindPath(root.left,target);
        FindPath(root.right,target);
        list.remove(list.size()-1);
       return listAll;
    }
}

八、 重建二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
       return reConstructBinaryTree(pre,0,pre.length-1,in,0,in.length-1);
   }
   public TreeNode reConstructBinaryTree(int [] pre,int startpre,int endpre,int [] in,int startin,int endin){
       if(startpre > endpre || startin > endin){
           return null;
       }
       TreeNode root = new TreeNode(pre[startpre]);
       for(int i =startin;i<=endin;i++){
           if(in[i] == pre[startpre]){
               root.left = reConstructBinaryTree(pre,startpre+1,startpre+i-startin,in,startin,i-1);
               root.right = reConstructBinaryTree(pre,startpre+i-startin+1,endpre,in,i+1,endin);
           }
       }
       return root;
   }

九、 二叉搜索树的后序遍历序列 

public boolean VerifySquenceOfBST(int [] sequence) {
       if(sequence.length==0)
              return false;
        int len = sequence.length-1;
        return split(sequence,0,len);
}
public boolean split(int [] sequence,int start,int end){
    if(start>=end)
        return true;
    int center = start;
    while(sequence[center]<sequence[end]&&center<end){
        center++;
    }
    for(int i=center;i<end;i++){
        if(sequence[i]<sequence[end]){
            return false;
        }
    }
    return split(sequence,start,center-1)&&split(sequence,center,end-1);

}

十、二叉树的序列化和反序列化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public String serialize(TreeNode root) {
        if (root == null) {
            return null;
        }
        // 利用二叉树的层次遍历方式进行序列化
        StringBuilder res = new StringBuilder();
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while (!queue.isEmpty()) {
            TreeNode node = queue.remove();
            if (node != null) {
                res.append(node.val).append(",");
                queue.add(node.left);
                queue.add(node.right);
            } else {
                res.append("null,");
            }
        }
        return res.toString();
    }

反序列化：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
public TreeNode deserialize(String data) {
        if (data == null || data.length() == 0) {
            return null;
        }
        String[] dataArr = data.split(",");
        // 层次遍历逆向还原二叉树
        int index = 0;
        TreeNode root = toNode(dataArr[index]);
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while (index < dataArr.length - 2 && !queue.isEmpty()) {
            TreeNode cur = queue.remove();
            // 添加左子节点
            TreeNode leftNode = toNode(dataArr[++index]);
            cur.left = leftNode;
            // 队列中的节点用于为其赋值孩子节点，若该节点本身为 null，
            // 没有孩子节点，便不再添加到队列中，下同理
            if (leftNode != null) {
                queue.add(leftNode);
            }
            // 添加右子节点
            TreeNode rightNode = toNode(dataArr[++index]);
            cur.right = rightNode;
            if (rightNode != null) {
                queue.add(rightNode);
            }
        }
        return root;
    }

private TreeNode toNode(String val) {
    if (!"null".equals(val)) {
        return new TreeNode(Integer.parseInt(val));
    } else {
        return null;
    }
}
-------------本文结束感谢您的阅读-------------
0%