Hashmap源码实现原理

发表于 | 阅读数
字数统计: 4.4k | 阅读时长 ≈ 19

首先下面有一段最基本的hashmap操作的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
package HashMaptest;

import java.util.HashMap;
import java.util.Iterator;
import java.util.Map;

public class HashmapTest {
	public static void main(String[] args){
		Map<Integer,String> hashmap=new HashMap<Integer,String>();
		hashmap.put(1,"jack");
		hashmap.put(1,"Jack");
		hashmap.put(2,"tom");
		hashmap.put(3,"Tony");
		hashmap.put(4,"");
		
		// 1. 通过Map.keySet遍历key和value：
		for(int key:hashmap.keySet()){
			System.out.println(key+":"+hashmap.get(key));
		}
//		 //2. 通过Map.entrySet使用iterator遍历key和value：
//        Iterator<Map.Entry<Integer, String>> it = hashmap.entrySet().iterator();
//        while (it.hasNext()){
//            Map.Entry<Integer, String> entry = it.next();
//            System.out.println("key: "+ entry.getKey() + "; value: " + entry.getValue());
//        }
// 
//        //3. 通过Map.entrySet遍历key和value
//        for(Map.Entry<Integer, String> entry : hashmap.entrySet()){
//            System.out.println("key: "+ entry.getKey() + "; value: " + entry.getValue());
//        }
// 
//        //4. 通过Map.values()遍历所有的value，但不能遍历key
//        for (String value : hashmap.values()) {
//            System.out.println("value: "+value);
//        }
	
	}

}

输出结果：

image-20200218170542493

代码比较简单就是向hashmap中存放了4组值，可以看到允许插入空值，并且相同的key会覆盖（输出的是Jack而不是jack）然后遍历一遍hashmap（正好复习了一遍hashmap的4种遍历方法）。

1. hashmap简介

HashMap基于哈希表的Map接口实现，是以key-value存储形式存在。（除了不同步和允许使用 null 之外，HashMap 类与 Hashtable 大致相同。)

HashMap 的实现不是同步的，这意味着它不是线程安全的。它的key、value都可以为null。此外，HashMap中的映射不是有序的。在 JDK1.8 中，HashMap 是由 数组+链表+红黑树构成，新增了红黑树作为底层数据结构，结构变得复杂了，但是效率也变的更高效。

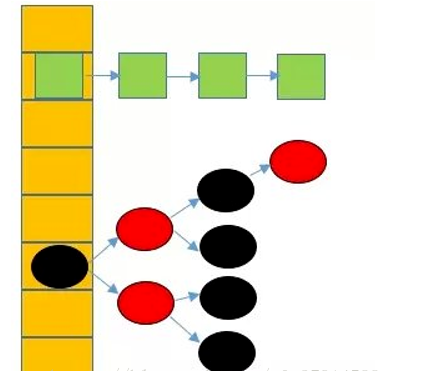
哈希桶就是数组里面的一个位置中所占所有数据，例如，下图中，绿色节点所占的该数组的位置，以及它连接的链表，整体为一个哈希桶。

image-20200218172233845

2.属性

我们直接来看源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public class HashMap<K,V> extends AbstractMap<K,V>
    implements Map<K,V>, Cloneable, Serializable {
    //序列号，序列化的时候使用。
    private static final long serialVersionUID = 362498820763181265L;
    /**默认容量，1向左移位4个，00000001变成00010000，也就是2的4次方为16，使用移位是因为移位是计算机基础运算，效率比加减乘除快。**/
    static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;
    //最大容量，2的30次方。
    static final int MAXIMUM_CAPACITY = 1 << 30;
    //加载因子，用于扩容使用。
    static final float DEFAULT_LOAD_FACTOR = 0.75f;
    //当某个桶节点数量大于8时，会转换为红黑树。
    static final int TREEIFY_THRESHOLD = 8;
    //当某个桶节点数量小于6时，会转换为链表，前提是它当前是红黑树结构。
    static final int UNTREEIFY_THRESHOLD = 6;
    //当整个hashMap中元素数量大于64时，也会进行转为红黑树结构。
    static final int MIN_TREEIFY_CAPACITY = 64;
    //存储元素的数组，transient关键字表示该属性不能被序列化
    transient Node<K,V>[] table;
    //将数据转换成set的另一种存储形式，这个变量主要用于迭代功能。
    transient Set<Map.Entry<K,V>> entrySet;
    //元素数量
    transient int size;
    //统计该map修改的次数
    transient int modCount;
    //临界值，也就是元素数量达到临界值时，会进行扩容。
    int threshold;
    //也是加载因子，只不过这个是变量。
    final float loadFactor;

在这里说一下加载因子

何为加载因子？

加载因子是表示Hsah表中元素的填满的程度.若:加载因子越大,填满的元素越多,好处是,空间利用率高了,但:冲突的机会加大了.反之,加载因子越小,填满的元素越少,好处是:冲突的机会减小了,但:空间浪费多了.

冲突的机会越大,则查找的成本越高.反之,查找的成本越小.因而,查找时间就越小.

因此,必须在 “冲突的机会”与”空间利用率”之间寻找一种平衡与折衷. 这种平衡与折衷本质上是数据结构中有名的”时-空”矛盾的平衡与折衷.

HashMap默认的加载因子是0.75，最大容量是16，因此可以得出HashMap的默认容量是：0.75*16=12。

用户可以自定义最大容量和加载因子。

3.构造方法

hashmap一共有4种构造法

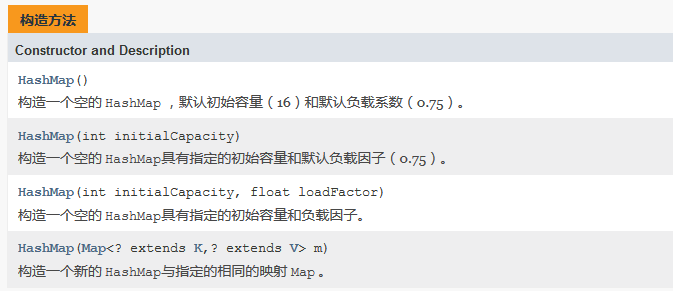
image-20200218174448495

源码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public HashMap() {
    this.loadFactor = DEFAULT_LOAD_FACTOR; 
}
 
 
public HashMap(int initialCapacity) {
    this(initialCapacity, DEFAULT_LOAD_FACTOR);
}
 
 
public HashMap(int initialCapacity, float loadFactor) {
    if (initialCapacity < 0)
        throw new IllegalArgumentException("Illegal initial capacity: " +
                                           initialCapacity);
    if (initialCapacity > MAXIMUM_CAPACITY)
        initialCapacity = MAXIMUM_CAPACITY;
    if (loadFactor <= 0 || Float.isNaN(loadFactor))
        throw new IllegalArgumentException("Illegal load factor: " +
                                           loadFactor);
    this.loadFactor = loadFactor;
    this.threshold = tableSizeFor(initialCapacity);
}

第一个，空参构造，使用默认的加载因子0.75；

第二个，设置初始容量，并使用默认的加载因子；

第三个，设置初始容量和加载因子，其实第二个构造方法也是调用了第三个。下面，在看看最后一个构造函数。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public HashMap(Map<? extends K, ? extends V> m) {
    this.loadFactor = DEFAULT_LOAD_FACTOR;
    putMapEntries(m, false);
}
 
 
final void putMapEntries(Map<? extends K, ? extends V> m, boolean evict) {
    //获取该map的实际长度
    int s = m.size();
    if (s > 0) {
        //判断table是否初始化，如果没有初始化
        if (table == null) { // pre-size
            /**求出需要的容量，因为实际使用的长度=容量*0.75得来的，+1是因为小数相除，基本都不会是整数，容量大小不能为小数的，后面转换为int，多余的小数就要被丢掉，所以+1，例如，map实际长度22，22/0.75=29.3,所需要的容量肯定为30，有人会问如果刚刚好除得整数呢，除得整数的话，容量大小多1也没什么影响**/
            float ft = ((float)s / loadFactor) + 1.0F;
            //判断该容量大小是否超出上限。
            int t = ((ft < (float)MAXIMUM_CAPACITY) ?
                     (int)ft : MAXIMUM_CAPACITY);
            /**对临界值进行初始化，tableSizeFor(t)这个方法会返回大于t值的，且离其最近的2次幂，例如t为29，则返回的值是32**/
            if (t > threshold)
                threshold = tableSizeFor(t);
        }
        //如果table已经初始化，则进行扩容操作，resize()就是扩容。
        else if (s > threshold)
            resize();
        //遍历，把map中的数据转到hashMap中。
        for (Map.Entry<? extends K, ? extends V> e : m.entrySet()) {
            K key = e.getKey();
            V value = e.getValue();
            putVal(hash(key), key, value, false, evict);
        }
    }
}

该构造函数，传入一个Map，然后把该Map转为hashMap，resize方法在下面添加元素的时候会详细讲解，在上面中entrySet方法会返回一个Set<Map.Entry<K, V>>，泛型为Map的内部类Entry，它是一个存放key-value的实例，也就是Map中的每一个key-value就是一个Entry实例，为什么使用这个方式进行遍历，因为效率高，具体自己百度一波，putVal方法把取出来的每个key-value存入到hashMap中，待会会仔细讲解。

构造函数和属性讲得差不多了，下面要讲解的是增删改查的操作以及常用的、重要的方法，毕竟里面的方法太多了，其它的就自己去看看吧。

4.添加元素

添加元素也就是put（）方法，在讲解put之前我们要看看hash方法如何计算哈希值的

1
2
3
4
5
static final int hash(Object key) {
    int h;
    /**先获取到key的hashCode，然后进行移位再进行异或运算，为什么这么复杂，不用想肯定是为了减少hash冲突**/
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

接下来看put方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
public V put(K key, V value) {
        /**四个参数，第一个hash值，第四个参数表示如果该key存在值，如果为null的话，则插入新的value，最后一个参数，在hashMap中没有用，可以不用管，使用默认的即可**/
        return putVal(hash(key), key, value, false, true);
    }
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
               boolean evict) {
    //tab 哈希数组，p 该哈希桶的首节点，n hashMap的长度，i 计算出的数组下标
    Node<K,V>[] tab; Node<K,V> p; int n, i;
    //获取长度并进行扩容，使用的是懒加载，table一开始是没有加载的，等put后才开始加载
    if ((tab = table) == null || (n = tab.length) == 0)
        n = (tab = resize()).length;
    /**如果计算出的该哈希桶的位置没有值，则把新插入的key-value放到此处，此处就算没有插入成功，也就是发生哈希冲突时也会把哈希桶的首节点赋予p**/
    if ((p = tab[i = (n - 1) & hash]) == null)
        tab[i] = newNode(hash, key, value, null);
    //发生哈希冲突的几种情况
    else {
        // e 临时节点的作用， k 存放该当前节点的key 
        Node<K,V> e; K k;
        //第一种，插入的key-value的hash值，key都与当前节点的相等，e = p，则表示为首节点
        if (p.hash == hash &&
            ((k = p.key) == key || (key != null && key.equals(k))))
            e = p;
        //第二种，hash值不等于首节点，判断该p是否属于红黑树的节点
        else if (p instanceof TreeNode)
            /**为红黑树的节点，则在红黑树中进行添加，如果该节点已经存在，则返回该节点（不为null），该值很重要，用来判断put操作是否成功，如果添加成功返回null**/
            e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
        //第三种，hash值不等于首节点，不为红黑树的节点，则为链表的节点
        else {
            //遍历该链表
            for (int binCount = 0; ; ++binCount) {
                //如果找到尾部，则表明添加的key-value没有重复，在尾部进行添加
                if ((e = p.next) == null) {
                    p.next = newNode(hash, key, value, null);
                    //判断是否要转换为红黑树结构
                    if (binCount >= TREEIFY_THRESHOLD - 1) 
                        treeifyBin(tab, hash);
                    break;
                }
                //如果链表中有重复的key，e则为当前重复的节点，结束循环
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    break;
                p = e;
            }
        }
        //有重复的key，则用待插入值进行覆盖，返回旧值。
        if (e != null) { 
            V oldValue = e.value;
            if (!onlyIfAbsent || oldValue == null)
                e.value = value;
            afterNodeAccess(e);
            return oldValue;
        }
    }
    //到了此步骤，则表明待插入的key-value是没有key的重复，因为插入成功e节点的值为null
    //修改次数+1
    ++modCount;
    //实际长度+1，判断是否大于临界值，大于则扩容
    if (++size > threshold)
        resize();
    afterNodeInsertion(evict);
    //添加成功
    return null;
}

上面就是具体的元素添加，在元素添加里面涉及到扩容，我们来看看扩容方法resize。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
final Node<K,V>[] resize() {
    //把没插入之前的哈希数组做我诶oldTal
    Node<K,V>[] oldTab = table;
    //old的长度
    int oldCap = (oldTab == null) ? 0 : oldTab.length;
    //old的临界值
    int oldThr = threshold;
    //初始化new的长度和临界值
    int newCap, newThr = 0;
    //oldCap > 0也就是说不是首次初始化，因为hashMap用的是懒加载
    if (oldCap > 0) {
        //大于最大值
        if (oldCap >= MAXIMUM_CAPACITY) {
            //临界值为整数的最大值
            threshold = Integer.MAX_VALUE;
            return oldTab;
        }
        //标记##，其它情况，扩容两倍，并且扩容后的长度要小于最大值，old长度也要大于16
        else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
                 oldCap >= DEFAULT_INITIAL_CAPACITY)
            //临界值也扩容为old的临界值2倍
            newThr = oldThr << 1; 
    }
    /**如果oldCap<0，但是已经初始化了，像把元素删除完之后的情况，那么它的临界值肯定还存在，        
       如果是首次初始化，它的临界值则为0
    **/
    else if (oldThr > 0) 
        newCap = oldThr;
    //首次初始化，给与默认的值
    else {               
        newCap = DEFAULT_INITIAL_CAPACITY;
        //临界值等于容量*加载因子
        newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
    }
    //此处的if为上面标记##的补充，也就是初始化时容量小于默认值16的，此时newThr没有赋值
    if (newThr == 0) {
        //new的临界值
        float ft = (float)newCap * loadFactor;
        //判断是否new容量是否大于最大值，临界值是否大于最大值
        newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
                  (int)ft : Integer.MAX_VALUE);
    }
    //把上面各种情况分析出的临界值，在此处真正进行改变，也就是容量和临界值都改变了。
    threshold = newThr;
    //表示忽略该警告
    @SuppressWarnings({"rawtypes","unchecked"})
        //初始化
        Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
    //赋予当前的table
    table = newTab;
    //此处自然是把old中的元素，遍历到new中
    if (oldTab != null) {
        for (int j = 0; j < oldCap; ++j) {
            //临时变量
            Node<K,V> e;
            //当前哈希桶的位置值不为null，也就是数组下标处有值，因为有值表示可能会发生冲突
            if ((e = oldTab[j]) != null) {
                //把已经赋值之后的变量置位null，当然是为了好回收，释放内存
                oldTab[j] = null;
                //如果下标处的节点没有下一个元素
                if (e.next == null)
                    //把该变量的值存入newCap中，e.hash & (newCap - 1)并不等于j
                    newTab[e.hash & (newCap - 1)] = e;
                //该节点为红黑树结构，也就是存在哈希冲突，该哈希桶中有多个元素
                else if (e instanceof TreeNode)
                    //把此树进行转移到newCap中
                    ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
                else { /**此处表示为链表结构，同样把链表转移到newCap中，就是把链表遍历后，把值转过去，在置位null**/
                    Node<K,V> loHead = null, loTail = null;
                    Node<K,V> hiHead = null, hiTail = null;
                    Node<K,V> next;
                    do {
                        next = e.next;
                        if ((e.hash & oldCap) == 0) {
                            if (loTail == null)
                                loHead = e;
                            else
                                loTail.next = e;
                            loTail = e;
                        }
                        else {
                            if (hiTail == null)
                                hiHead = e;
                            else
                                hiTail.next = e;
                            hiTail = e;
                        }
                    } while ((e = next) != null);
                    if (loTail != null) {
                        loTail.next = null;
                        newTab[j] = loHead;
                    }
                    if (hiTail != null) {
                        hiTail.next = null;
                        newTab[j + oldCap] = hiHead;
                    }
                }
            }
        }
    }
    //返回扩容后的hashMap
    return newTab;
}

5.删除

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
public V remove(Object key) {
    //临时变量
    Node<K,V> e;
    /**调用removeNode(hash(key), key, null, false, true)进行删除，第三个value为null，表示，把key的节点直接都删除了，不需要用到值，如果设为值，则还需要去进行查找操作**/
    return (e = removeNode(hash(key), key, null, false, true)) == null ?
        null : e.value;
}

/**第一参数为哈希值，第二个为key，第三个value，第四个为是为true的话，则表示删除它key对应的value，不删除key,第四个如果为false，则表示删除后，不移动节点**/
final Node<K,V> removeNode(int hash, Object key, Object value,
                           boolean matchValue, boolean movable) {
    //tab 哈希数组，p 数组下标的节点，n 长度，index 当前数组下标
    Node<K,V>[] tab; Node<K,V> p; int n, index;
    //哈希数组不为null，且长度大于0，然后获得到要删除key的节点所在是数组下标位置
    if ((tab = table) != null && (n = tab.length) > 0 &&
        (p = tab[index = (n - 1) & hash]) != null) {
        //nodee 存储要删除的节点，e 临时变量，k 当前节点的key，v 当前节点的value
        Node<K,V> node = null, e; K k; V v;
        //如果数组下标的节点正好是要删除的节点，把值赋给临时变量node
        if (p.hash == hash &&
            ((k = p.key) == key || (key != null && key.equals(k))))
            node = p;
        //也就是要删除的节点，在链表或者红黑树上，先判断是否为红黑树的节点
        else if ((e = p.next) != null) {
            if (p instanceof TreeNode)
                //遍历红黑树，找到该节点并返回
                node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
            else { //表示为链表节点，一样的遍历找到该节点
                do {
                    if (e.hash == hash &&
                        ((k = e.key) == key ||
                         (key != null && key.equals(k)))) {
                        node = e;
                        break;
                    }
                    /**注意，如果进入了链表中的遍历，那么此处的p不再是数组下标的节点，而是要删除结点的上一个结点**/
                    p = e;
                } while ((e = e.next) != null);
            }
        }
        //找到要删除的节点后，判断!matchValue，我们正常的remove删除，!matchValue都为true
        if (node != null && (!matchValue || (v = node.value) == value ||
                             (value != null && value.equals(v)))) {
            //如果删除的节点是红黑树结构，则去红黑树中删除
            if (node instanceof TreeNode)
                ((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
            //如果是链表结构，且删除的节点为数组下标节点，也就是头结点，直接让下一个作为头
            else if (node == p)
                tab[index] = node.next;
            else /**为链表结构，删除的节点在链表中，把要删除的下一个结点设为上一个结点的下一个节点**/
                p.next = node.next;
            //修改计数器
            ++modCount;
            //长度减一
            --size;
            /**此方法在hashMap中是为了让子类去实现，主要是对删除结点后的链表关系进行处理**/
            afterNodeRemoval(node);
            //返回删除的节点
            return node;
        }
    }
    //返回null则表示没有该节点，删除失败
    return null;
}

删除还有clear方法，把所有的数组下标元素都置位null，下面在来看看较为简单的获取元素与修改元素操作。

6.获取元素：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public V get(Object key) {
    Node<K,V> e;
    //也是调用getNode方法来完成的
    return (e = getNode(hash(key), key)) == null ? null : e.value;
}
 
final Node<K,V> getNode(int hash, Object key) {
    //first 头结点，e 临时变量，n 长度,k key
    Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
    //头结点也就是数组下标的节点
    if ((tab = table) != null && (n = tab.length) > 0 &&
        (first = tab[(n - 1) & hash]) != null) {
        //如果是头结点，则直接返回头结点
        if (first.hash == hash && 
            ((k = first.key) == key || (key != null && key.equals(k))))
            return first;
        //不是头结点
        if ((e = first.next) != null) {
            //判断是否是红黑树结构
            if (first instanceof TreeNode)
                //去红黑树中找，然后返回
                return ((TreeNode<K,V>)first).getTreeNode(hash, key);
            do { //链表节点，一样遍历链表，找到该节点并返回
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    return e;
            } while ((e = e.next) != null);
        }
    }
    //找不到，表示不存在该节点
    return null;
}

7.修改元素

元素的修改也是put方法，因为key是唯一的，所以修改元素，是把新值覆盖旧值。

原文链接：https://blog.csdn.net/m0_37914588/article/details/82287191

-------------本文结束感谢您的阅读-------------
0%